Solving Inefficiency of Self-supervised Representation Learning 论文笔记
bibtex
1 | |
Introduction
知名的自监督方法:MoCo v1/v2, SimCLR, BYOL, SimSiam
自监督模型较有监督模型花费10倍的时间,在ImageNet上训练ResNet-50通常要100轮,但用SimCLR和BYOL方式训练ResNet-50需要1000轮,用MoCo v2需要800轮。
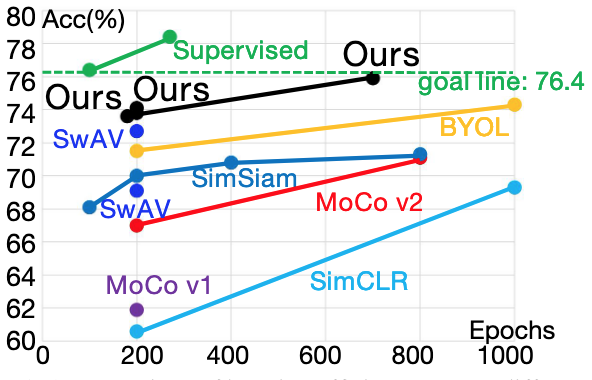
作者提出自监督方法存在着两种问题,即欠聚集问题(Under-clustering)和过聚集问题(Over-clustering)。自监督训练的目标是减少正例之间的距离,增大负例之间的距离。欠聚集问题会导致模型难以发现不同类间样本的相异处,过聚集问题会导致模型到有害的不必要的表示学习。作者认为现有的自监督方法难以解决过聚集以及欠聚集问题,所以学习效率依然很低。
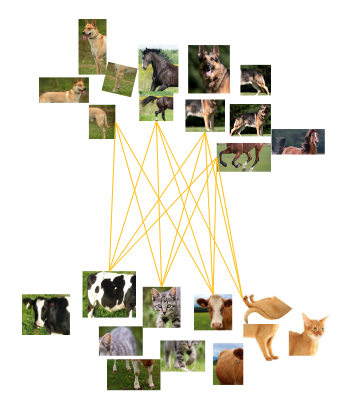
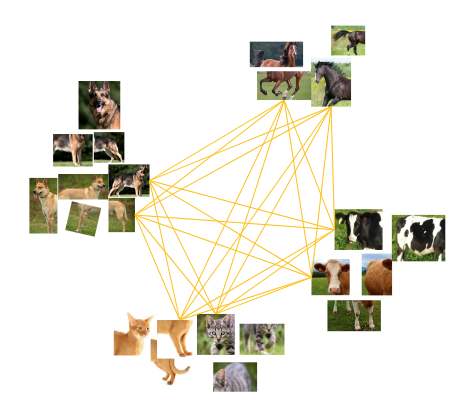
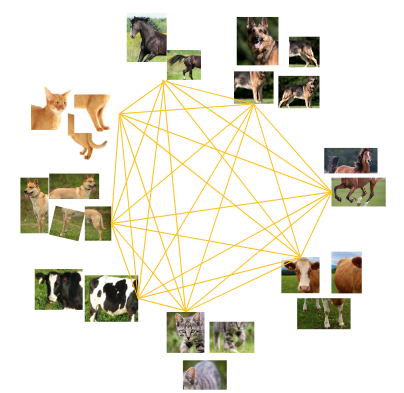
作者提出了一种简单的truncated triplet loss,能够最大化每个三胞胎单元中的正对与负对,同时改善了传统triplet loss存在的只解决欠聚集而难以解决过聚集的问题。
作者提出的创新点:
- 作者分析了现存最好性能的对比学习方法并推断出其学习效率差的原因是欠聚合与过聚合问题,会导致不必要的有害的表示学习,导致模型仅仅能够记住数据本身。
- 为了强调欠聚合与过聚合问题,作者提出了使用truncated triplet loss的自监督框架。作者使用triplet loss来突出大量负例的作用从而避免欠聚合,同时用截断的方法来避免模型的过聚合。
- 作者提高了自监督模型的学习效率,在几种大规模数据集(ImageNet、SYSU-30k、COCO 2017)以及不同的下游任务上达到了SOTA的性能。
Related Work
Contrastive LearningSimCLR, Mean Teacher (NIPS 2017), MoCo v1/v2, Exemplar-CNN, BYOL, SimSiam, False Negative Cancellation, Debiased CL, Hard Negative Samples. 作者认为上述的改进方法中Loss都过于复杂,作者认为提出的truncated triplet loss非常简单。
Triplet Loss最大化正对与负对间的相对距离,传统的triplet loss会导致过聚集,作者利用伯努利分布模型保证使用truncated triplet loss能够解决过聚集问题。
Self-supervised Representation Learning
InfoNCE接近1,并促使
不充足的正例或负例会导致欠聚集,不同类别会出现交叉的现象。
过聚集压倒性的、过多的负例会导致过聚集,可能会把很少量的样本聚集为一组。
理想情况使用正确数目的负例来进行训练,能够确保相同类别的能够被聚集在一组,同时不同类别之间存在一定间距。
Triplet Loss对三元组
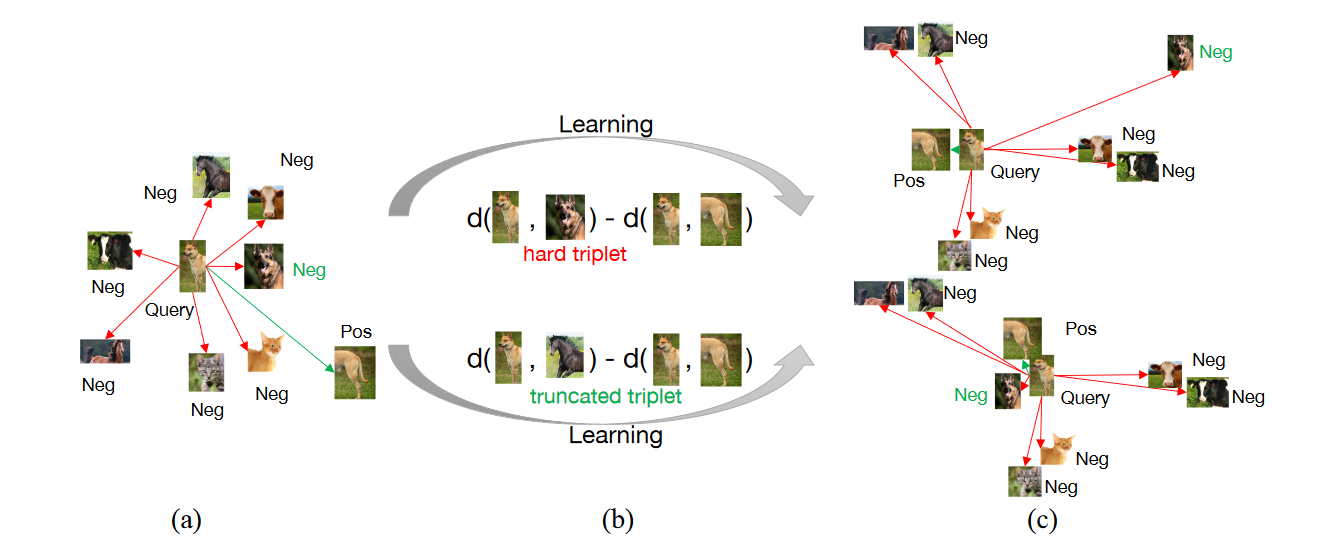
作者提出了truncated triplet loss,指出选用具有代表性的负例计入损失,
- 计算出所有负例与样本的距离
; - 用升序排序
; - 用两种方式获得
: - rank-k triplet loss,即
- smoothed-rank-k triplet loss,即
- rank-k triplet loss,即
作者实际采用余弦距离作为
Main results
数据增广:randomly cropping, randomly resizing, randomly flipping horizontally, arbitrary gray scaling, stochastic color jittering, Gaussian blurring, and solarization.
其他:104张图片/GPU/批;最大100轮训练;学习率从4.8开始用cosine annealing下降;优化器用LARS,weight decay为1e-6,momentum为0.9;backbone为ResNet-50.
实验部分不赘述,详见论文原文。